Warning: fopen(/home/virtual/epih/journal/upload/ip_log/ip_log_2024-12.txt): failed to open stream: Permission denied in /home/virtual/lib/view_data.php on line 95 Warning: fwrite() expects parameter 1 to be resource, boolean given in /home/virtual/lib/view_data.php on line 96 Assessing measurement error in surveys using latent class analysis: application to self-reported illicit drug use in data from the Iranian Mental Health Survey
Skip Navigation
Skip to contents

Epidemiol Health : Epidemiology and Health

OPEN ACCESS
SEARCH
Search
Advanced Search
mobile menu button

Articles

Page Path
HOME > Epidemiol Health > Volume 38; 2016 > Article
Method
 Assessing measurement error in surveys using latent class analysis: application to self-reported illicit drug use in data from the Iranian Mental Health Survey
Kazem Khalagi1orcid, Mohammad Ali Mansournia1orcid, Afarin Rahimi-Movaghar2orcid, Keramat Nourijelyani1orcid, Masoumeh Amin-Esmaeili2orcid, Ahmad Hajebi3,4orcid, Vandad Sharif5,6orcid, Reza Radgoodarzi7orcid, Mitra Hefazi7orcid, Abbas Motevalian3,8orcid
Epidemiol Health 2016;38:e2016013.
DOI: https://doi.org/10.4178/epih.e2016013
Published online: April 10, 2016

1Department of Epidemiology and Biostatistics, School of Public Health, Tehran University of Medical Sciences, Tehran, Iran

2Iranian National Center for Addiction Studies, Tehran University of Medical Sciences, Tehran, Iran

3Addiction and High Risk Behavior Research Center, Iran University of Medical Sciences, Tehran, Iran

4Department of Psychiatry, Iran University of Medical Sciences, Tehran, Iran

5Psychiatry and Psychology Research Center, Tehran University of Medical Sciences, Tehran, Iran

6Department of Psychiatry, Tehran University of Medical Sciences, Tehran, Iran

7Department for Mental Health and Substance Use, Iranian Research Center for HIV/AIDS, Iranian Institute for Reduction of High-Risk Behaviors, Tehran University of Medical Sciences, Tehran, Iran

8Department of Epidemiology, School of Public Health, Iran University of Medical Sciences, Tehran, Iran

Correspondence: Seyed-Abbas Motevalian  Department of Epidemiology, School of Public Health, Iran University of Medical Sciences, P.O. Box 1449614535, Tehran, Iran  Tel: +98-21-86704704, Fax: +98-21-88622703, E-mail: amotevalian@yahoo.com
• Received: March 10, 2016   • Accepted: April 10, 2016

©2016, Korean Society of Epidemiology

This is an open-access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

prev next
  • 17,302 Views
  • 260 Download
  • 1 Scopus
Full Article

Download PDF Download PDF

  • Latent class analysis (LCA) is a method of assessing and correcting measurement error in surveys. The local independence assumption in LCA assumes that indicators are independent from each other condition on the latent variable. Violation of this assumption leads to unreliable results. We explored this issue by using LCA to estimate the prevalence of illicit drug use in the Iranian Mental Health Survey. The following three indicators were included in the LCA models: five or more instances of using any illicit drug in the past 12 months (indicator A), any use of any illicit drug in the past 12 months (indicator B), and the self-perceived need of treatment services or having received treatment for a substance use disorder in the past 12 months (indicator C). Gender was also used in all LCA models as a grouping variable. One LCA model using indicators A and B, as well as 10 different LCA models using indicators A, B, and C, were fitted to the data. The three models that had the best fit to the data included the following correlations between indicators: (AC and AB), (AC), and (AC, BC, and AB). The estimated prevalence of illicit drug use based on these three models was 28.9%, 6.2% and 42.2%, respectively. None of these models completely controlled for violation of the local independence assumption. In order to perform unbiased estimations using the LCA approach, the factors violating the local independence assumption (behaviorally correlated error, bivocality, and latent heterogeneity) should be completely taken into account in all models using well-known methods.
  • Keywords: Surveys and questionnaires, Bias, Outcome measurement errors, Latent class analysis, Self report, Substance-related disorders
Measurement error is a major source of systematic error when estimating variables, especially those reflecting outcomes related to sensitive topics in surveys. This error refers to the difference between the true value of an outcome and what is obtained from a measuring tool [1,2]. Such errors may cause misclassification in categorical outcomes. The measuring tool, the interviewers, the respondents, and the data collection style (in person, telephone, web, etc.) are among the major sources of this type of error in surveys [1-3]. This type of error in categorical data causes bias and reduces the precision of the estimation [4,5]. Despite the range of measures that may be taken in the design and execution of surveys, such errors are inevitable, especially for sensitive outcomes, such as risky behaviors involving sexual relations and the use of illicit drugs. In such situations, the assessment and correction of measurement error becomes more important.
If a survey contains at least two measurements of a categorical outcome, one of which is a gold standard (i.e., a measurement with negligible error), the classification error of another tool can easily be estimated and corrected. This method of assessing classification error is known as the finite fixture approach [1]. However, using this approach to assess and correct classification errors is not possible in most cases due to the lack of a gold standard or its cost. Latent class analysis (LCA) is a suitable solution for assessing and correcting the classification error of any measurement in a survey study in which different wording is used to obtain repeated measurements of an outcome when none of the measurements is a gold standard [1,3]. LCA was first introduced by Lazarsfeld & Henry [6] for classification error assessment in 1968. Extensive experience has been accumulated regarding its advantages and limitations. The use of LCA can be highly suitable for the quantitative analysis of classification error in survey data if the assumptions of the model are logically established. Otherwise, its incorrect use may lead to invalid results, similarly to any other modeling approach [3].
This paper aims to introduce the LCA approach for assessing and correcting classification error in the estimation of categorical outcomes in surveys through focusing on its required assumptions, which should be considered in order to use it correctly. As an example, we used LCA to estimate the prevalence of illicit drug use in the past 12 months based on data from the Iranian Mental Health Survey (IranMHS) and we discuss the essential assumptions involved in doing so.
Several indicator (manifest) variables are used in the LCA approach of estimating a latent variable [1]. This method assumes a relationship between the classifications of the indicator variables and the unobserved latent classes of an outcome variable [7,8].
In order to use an LCA model to assess and correct the measurement error of a categorical outcome in survey data, two or more indicators should measure the variable, and none of them should necessarily be a gold standard [9]. The other indicators can be provided by re-measuring the outcome using another survey a few weeks later, or by measuring the outcome in a survey through multiple items that use different wording. The first method is difficult and costly to implement, and the short interval between the two measurements may lead to interrelated responses due to the respondent’s memories. The limitations of the second method include the possibility that respondents may exhibit a lack of cooperativity in answering similar questions that seem to be redundant, as well as the possibility that none of the items may accurately measure a variable that is necessarily latent [3].
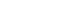
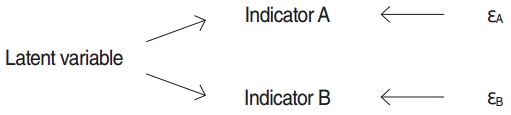
In standard LCA models, the local independence assumption is used to provide the degrees of freedom required to estimate the parameters of the model [7,10]. According to this assumption, the indicators are independent from each other condition on the latent variable and 100% of the correlation among indicators is justified by the latent variable (Figure 1) [3,7,10]. As illustrated in Figure 1, if a condition is placed on the latent variable, the connecting path between indicators A and B will be closed completely. Most statistical software and packages used to carry out LCA analysis have been designed based on this assumption.
It may not be possible to confirm the local independence assumption when using LCA models to assess measurement error in survey data [3,7]. Violation of the assumption occurs for several possible reasons. One factor is behaviorally correlated error, which occurs when a respondent, for instance, answers indicators A and B in an intentionally incorrect manner or when the answers to both indicators are incorrect because the respondent has not understood the concept underlying indicators A and B. Therefore, the indicators A and B are dependent on each other condition on the latent variable, as shown in Figure 2A. The first scenario is probable when repeating a measurement in a survey and the second scenario is probable both when repeating measurement in a survey and when performing re-measurement using another survey [3,9]. A second factor is bivocality, which occurs when the indicators do not necessarily measure a common latent variable. For example, indicator A measures latent variable X, while indicator B measures latent variable Y; in this scenario, the latent variables X and Y may be correlated, but not identical. In this scenario, indicators A and B are also correlated condition on the latent variable (Figure 2B). This situation is probable when repeated measurements are made in a single survey [3,9]. A third factor, latent heterogeneity, occurs when the classification errors of indicators changes at different levels of an unknown grouping variable in a population. For instance, it is evident that the probability that respondents with a low level of literacy may misunderstand a question is higher than the probability that highly literate respondents would have a similar misunderstanding (Figure 2C) [3,9].
If the possibility that the local independence assumption is violated is not considered in LCA models, measurement bias in estimating parameters such as the classification error rate of indicators or the prevalence of the outcome variable is not completely corrected. For instance, if a positive correlation is present between the classification errors of an indicator, those values for different indicators using an LCA model with the local independence assumption would be underestimated [11,12].
The use of latent class log-linear (LCLL) models provides the flexibility required for data analysis when the local independence assumption is not established [1]. The non-establishment of the local independence assumption can be taken into account in LCLL models by inserting interaction terms between indicators that are correlated due to bivocality or behaviorally correlated error [3]. It is possible to provide a suficient degree of freedom for LCLL models by inserting grouping variables to estimate the correlation parameters between indicators [7]. Of course, it is better to select the grouping variables from those that play a role in latent heterogeneity [3].
The IranMHS was a three-stage national household survey conducted from January to June 2011. The primary goal was to estimate the 12-month prevalence and severity of psychiatric disorders among the Iranian population aged 15 to 64 years. The validated Persian version of the paper-and-pencil interview form of the Composite International Diagnosis Interview version 2.1 (CIDI 2.1) was used as the main tool for diagnosing psychiatric disorders in this study. The CIDI 2.1 includes questions regarding drug and alcohol use disorders. The study design and field procedures have been published elsewhere [13].
We aimed to assess measurement errors in estimations of the prevalence of illicit drug use in the past 12 months in the IranMHS data using an LCA approach. The list of illicit drugs in the IranMHS included various forms of cannabis; amphetaminetype stimulants; opioids, including opium and heroin/crack of heroin [14]; the hallucinogens ecstasy and lysergic acid diethylamide; volatile solvents; and other illicit substances. The list did not include over-the-counter sedative/hypnotics and codeine-containing medications.
The LCA approach using LCLL models were used to fit the IranMHS data. A LCLL model was fit to this data using two indicators for illicit drug use in the past 12 months according to the IranMHS questionnaires, and 10 different LCLL models were also fitted to the data using three indicators. Moreover, a gender grouping variable was defined in order to account for latent heterogeneity and to increase the degrees of freedom of the models.
The following three indicators were used. Indicator A was based on answers to questions about the use of any kind of illicit drugs without a prescription more than five times in the past 12 months during a face-to-face interview in which the interviewee was presented with a list of the drugs in question. Indicator B was based on answers to 10 questions about the use of any kind of illicit drugs without a prescription at least one time in the past 12 months using a self-administered questionnaire. Indicator C corresponded to face-to-face questions about the respondent’s need to receive treatment for drug use and dependency over the past 12 months, or the use of any outpatient, inpatient, short-term residential, or traditional services due to drug use and dependency in the past 12 months. Receiving agonist maintenance treatment and membership in Narcotics Anonymous were excluded from indicator C because many people in these long-term treatment programs would be likely to have been abstinent from their primary drug for a long time. Definitions of these three indicators are presented in Appendix 1 based on the specific terms used in the IranMHS questionnaires.
Table 2 presents the characteristics of the 11 different LCLL models applied to the IranMHS data. In these models, Y denotes the real drug consumption status in the absence of classification errors, which is latent. Model 0 is a two-indicator model, while models 1-10 are three-indicator models. In all models, the amount of classification errors among indicators is expressed by the interaction terms (AY and BY in model 0; and AY, BY, and CY in models 1-10). In all models, GY indicates different estimates of the prevalence of illicit drug use according to gender after adjusting for classification errors. In models 0, 1, and 9, it was assumed that no correlation was present between the indicators condition on the latent status (the local independence assumption) [7,10]. In all models except models 9 and 10, it was assumed that the amount of classification errors for each indicator was the same in both genders. In models 2-8 and 10, different scenarios where the local independence assumption did not hold were imposed to the data. The interaction term between two indicators showed that a correlation was present between the two indicators condition on the latent Y variable. Model 9 was obtained by adding the interaction terms AG, BG, and CG to model 1. These terms imposed a specific kind of variability on the data in the amount of the classification error for each indicator between the two genders. For example, the BG term next to the BY term in model 9 in Table 2 implies that the multiplicative product of the odds of a false positive error in indicator B and the odds of a false negative error in indicator B was always constant for both genders. In order for this to have been the case, it would have been necessary (for example) for men who responded to indicator B with a higher false positive error probability than women to have also responded to the indicator with a lower false negative error probability. Thus, the above product of the odds shall remain constant for both genders. This is discussed in more detail in Biemer & Wiesen [7].
By adding the interaction terms (AC, AB) to model 9, model 10 was obtained, which also imposed the absence of the local independence assumption on the data. Two differences are present between model 10 and model 1: first, in model 10, it was assumed that the amount of the classification errors for each indicator varied with gender; second, in model 10, the local independence assumption no longer held.
In order to select the best three-indicator model in Table 2, the Lin & Dayton [15] criteria were used. Based on these criteria, all of the three-indicator models in Table 2 were identifiable, since the number of their parameters was smaller than the degrees of freedom (i.e., the number of cells in the ABCG cross table) [16,17]. However, model 7 had the lowest Bayesian information criterion (BIC), was selected as the best three-indicator model, and was then used to estimate the prevalence of illicit drug use after adjusting for the classification error and the sensitivity and specificity of each of the indicators.
The expectation maximization algorithm is the method we used to estimate the parameters of the models [10,17,18]. The non-parametric bootstrap 95% confidence intervals of the estimates of the two-indicator and the best three-indicator LCLL models were constructed through independent resampling of the province strata in the main data. This was due to the fact that the first stage of the sampling of the IranMHS was carried out using stratified sampling of the provinces. The multi-stage sampling design of the IranMHS was not taken into account in the estimations.
All statistical analyses were carried out in R software version 3.2.0 [19]. The emgllm function of the gllm package [20] was used to fit the LCLL models. Samples of the code used in the statistical analysis in R are presented in Appendix 2.
Ethics statement
The study protocol was approved by the institutional review board of Tehran University of Medical Sciences.
Indicators A and C were assessed based on face-to-face interviews with the participants. However, the questionnaire for indicator B was completed by the participants themselves and was put in a closed receptacle to protect their confidentiality. Table 1 presents the degree of disagreement among indicators A, B, and C for the use of any illicit drug in the IranMHS. Indicator B showed the highest degree of inconsistency with the other indicators.
As presented in Table 2, model 7 was selected as the best threeindicator model. This model took into account correlations between indicators A and C and indicators A and B in estimating the prevalence of illicit drug use in the past 12 months. An expert indicated that the estimated prevalence of illicit drug use by this model was unrealistically high.
Table 3 presents estimates of sensitivity and specificity (%) of the indicators after application of the two-indicator model using indicators A and B (model 0) and model 7 to the IranMHS data. The estimated specificity of all the indicators in models 0 and 7 was extremely high because the likelihood of a false positive response about the use of illicit drugs is very low. In contrast, the estimated sensitivity of the indicators in model 7 was much lower than in model 0, because in model 0, a correlation between the indicators was not imposed on the data, meaning that the false negative error of the indicators was underestimated.
The sensitivity of indicator B was higher than that of indicator A in model 0 and the two other indicators in model 7, and the sensitivity of indicator A was higher than that of indicator C in model 7. Since indicator B directly assessed the use of illicit drugs at least one time in the past 12 months using a self-administrated questionnaire, it had a better sensitivity than the other indicators. In contrast, since the indicator C asked about the perceived necessity of treatment or service using for substance-use disorders, and so ignored non-problematic drug users, it had the lowest sensitivity among the indicators in model 7.
In Table 4, estimates of the prevalence of illicit drug use employing the LCLL models with two and three indicators (adjusted for classification errors) and those using indicators A, B, and C (unadjusted) are presented by gender. After adjusting for classification errors in the self-report of illicit drug use, the estimated prevalence of drug use increased. This increase was lower in the LCLL model with two indicators than in the model with three indicators. The reason for this is that the measurement error correction in the LCLL model with two indicators was incomplete, because this model did not take into account the correlation between the indicators.
The findings presented in Table 4 also indicate that measurement error in self-reported illicit drug use was an important factor in underestimating the prevalence of the use of these drugs. Although the adoption of techniques such as self-administered questionnaires leads to a reduction in the occurrence of such errors in the course of research [21], it does not fully prevent them.
In the IranMHS data, the indicators used in the LCA models were bivocal because they did not measure a common latent variable. Indicator A measured the latent variable of more than five instances of using any illicit drug in the past 12 months. Indicator B measured the latent variable of at least one instance of using any illicit drug in the past 12 months. Indicator C measured the latent variable of the need for or the use of treatment services due to drug abuse and addiction in the past 12 months. The latent variable of indicator C is nested within the latent variable of indicator A, and the latent variable of indicator A is nested within the latent variable of indicator B. The correlation between the latent variables of indicators A and B was high, but the correlation between the latent variable of indicator C and the latent variables of the other two indicators was weaker. Therefore, indicator C was considered a weak indicator.
In contrast, behaviorally correlated error is expected to occur among the three indicators due to the nature of the questions, and in particular, the fact that they assessed illicit drug use. That is, if a respondent initially denies illicit drug use when answering indicator A, he or she would be expected to deny it deliberately when answering indicators B and C. However, this pattern may have occurred less for indicator C due to its indirect nature.
The incidence of bivocality and behaviorally correlated error among the IranMHS indicators indicate the non-establishment of the local independence assumption when using the LCA approach to analyze the data of this survey. As the correlation among the indicators in this survey was positive, it may be expected that failing to consider the violation of this assumption in LCA models would lead to bias in estimating the model parameters manifesting in the underestimation of the classification error of the indicators and, consequently, an incomplete correction of the estimated prevalence of drug use. In model 0, which only used indicators A and B along with a gender grouping variable for assessing and correcting classification error in the prevalence of illicit drug use (known as the Hui-Walter method [22]), the local independence assumption was imposed on the data. Therefore, it may be expected that the classification error rate of these two indicators would be underestimated and the estimation of the prevalence of drug use would be lower than the real rate due to incomplete correction. Only eight degrees of freedom are present in the two-indicator model along with one binary grouping variable, which was used to estimate its eight parameters, and it would not be possible to assess a correlation between indicators A and B through inserting an interaction term between them into the model due the insufficient degrees of freedom.
As sufficient degrees of freedom are present for estimating the parameters of correlation between indicators in the three-indicator models with one gender grouping variable (models 1-10), the non-establishment of the local independence assumption can be imposed on the data in these models. Among the three-indicator models presented in Table 2, the local independence assumption is established in models 1 and 9. Therefore, these two models, like the two-indicator model (model 0), are not suitable for the IranMHS data. Among the other three-indicator models, different modes of the non-establishment of the local independence assumption were imposed on the data. It was noted that variation was present in the estimated value of prevalence of drug use among models with different modes of correlation structure among the indicators. However, experts believe that the prevalence estimation obtained from the selected three-indicator model (model 7) is unlikely to be correct.
Indicators A and C in the IranMHS data showed the highest marginal correlation, and the correlation strength between indicators A and B was second-order. It was noticed that the BIC of the model with interaction term AC was the lowest and the BIC of the model with the interaction term BC was the highest in models 2-4, which only added one interaction term to the LCA models. The BIC of the model with AC and AB interaction terms was the lowest and the BIC of the model with AB and BC interaction terms was the highest among models 5-7, which added two interaction terms to the LCA models. This means that a lower BIC was obtained in the models in which the correlation structure between indicators had more conformity with the correlation structure in the data.
Both bivocality and behaviorally correlated error phenomena occurred in the IranMHS data; however, the correlation structure that emerged among the indicators due to these two phenomena did not correspond together. While bivocality was strong between indicators AC and BC, and weak between indicators AB, behaviorally corrected error was strong between indicators AC and AB, and weak between indicators BC. The correlation structure caused by behaviorally correlated error in the data exceeded that caused by bivocality. Therefore, some bivocality remained in the models with greater fitness with this type of correlation structure in the data (such as model 7, with the lowest BIC), that was not considered, and it may be expected to lead to estimations that are not completely unbiased.
In contrast, only the gender grouping variable was used in the LCA models for the IranMHS data. Statistically, this variable did not play a crucial role in creating latent heterogeneity (with respect to the BIC of models 9 and 10). One of the other factors that was probably involved in the incorrectness of estimations of the three-indicator model with lowest BIC (model 7) was the probability of latent heterogeneity in unknown variables that were not considered in analyzing the IranMHS data.
In order to obtain unbiased estimations when assessing and correcting classification errors in estimates of categorical outcomes in surveys using the LCA approach, the factors leading to violations of local independence (bivocality, behaviorally corrected error, and latent heterogeneity) should be considered in models. At least three indicators should be developed for a latent variable when designing survey studies, and these indicators should have univocality or at least minimum bivocality. Moreover, all variables for which the classification error of indicators is expected to be variable at their levels and consequently lead to latent heterogeneity should be identified and measured. Finally, well-known methods should be used for considering any factor violating the local independence assumption in models when analyzing survey data using LCA.
This work was supported by grants from Tehran University of Medical Sciences.

The authors have no conflicts of interest to declare for this study.

Figure 1.
The local independence assumption. ε, measurement error.
epih-38-e2016013f1.gif
Figure 2.
Types of violation of the local independence assumption. (A) Behaviorally correlated error, (B) bivocality, and (C) latent heterogeneity. ε, measurement error.
epih-38-e2016013f2.gif
Table 1.
Cross-tabulation of the three indicators of illicit drug use in the past 12 months
Indicator A Indicator C
 Total
Yes No
Yes Indicator B Yes 44 (37.6) 64 (54.7) 108 (92.3)
No 1 (0.9) 8 (6.8) 9 (7.7)
Total 45 (38.5) 72 (61.5) 117 (100)
No Indicator B Yes 3 (0.1) 114 (3.6) 117 (3.7)
No 18 (0.6) 3,018 (95.7) 3,036 (96.3)
Total 21 (0.7) 3,132 (99.3) 3,153 (100)
Total Indicator B Yes 47 (1.4) 178 (5.4) 225 (6.9)
No 19 (0.6) 3,026 (92.5) 3,045 (93.1)
Total 66 (2.0) 3,204 (98.0) 3,270 (100)

Values are presented as number (%).

Table 2.
Characteristics of alternative latent class log-linear models applied to the IranMHS data regarding illicit drug use
Model Degrees of freedom No. of parameters Deviance1 p-value of likelihood ratio test BIC + [2*ln (likelihood of saturated model)]2 Prevalence (adjusted for classification error, %)
Model 0 (AY, BY, GY) 0 8 1.70 0.99 66.44 6.14
Model 1 (AY, BY, CY, GY) 6 10 50.45 <0.001 131.38 5.56
Model 2: same as model 1 + (AB) 5 11 40.92 0.006 129.94 7.31
Model 3: same as model 1 +(BC) 5 11 50.37 <0.001 139.39 5.52
Model 4: same as model 1 + (AC) 5 11 19.90 0.53 108.92 6.18
Model 5: same as model 1 + (AC, BC) 4 12 15.77 0.73 112.88 6.23
Model 6: same as model 1 +(AB, BC) 4 12 38.84 0.007 135.95 7.98
Model 7: same as model 1 +(AC, AB) 4 12 7.43 1.00 104.54 28.87
Model 8: same as model 1 +(AC, BC, AB) 3 13 3.77 1.00 108.98 42.17
Model 9: same as model 1 +(AG, BG, CG) 3 13 9.22 0.97 114.42 3.55
Model 10: same as model 9+(AC, AB) 1 15 20.37 0.25 141.76 49.99

IranMHS, Iranian Mental Health Survey; BIC, Bayesian information criterion.

1 -2*(ln[likelihood of current model] – ln[likelihood of saturated model]).

2 The reason for replacing BIC with “BIC [2*ln(likelihood of saturated model)]” is explained in Appendix 3.

Table 3.
Estimated sensitivity and specificity (%) of indicators of illicit drug use in the past 12 months
Indicator By LCLL model with 2 indicators (model 0)
 By LCLL model with 3 indicators (model 7)
Sensitivity (95% CI) Specificity (95% CI) Sensitivity (95% CI) Specificity (95% CI)
A 58.29 (49.63, 67.53) 100.00 (reference) 12.39 (7.65, 34.45) 100.00 (reference)
B 92.32 (87.13, 96.82) 98.70 (98.01,99.38) 20.84 (13.57, 54.89) 98.79 (98.13, 99.40)
C - - 6.77 (4.03, 18.43) 99.91 (99.67, 100.00)

F195% CIs calculated using non-parametric bootstrapping with 500 iterations.

LCLL, latent class log-linear; CI, confidence interval.

Table 4.
Comparison of prevalence (%) estimates using indicators A, B, C and the LCLL models with two and three indicators for the use of any illicit drug in the past 12 months
Gender Indicator A
 Indicator B
 Indicator C
 LCLL (2-indicator)1
 LCLL (3-indicator)1
n Prevalence (95% CI) n Prevalence (95% CI) n Prevalence (95% CI) n Prevalence (95% CI) n Prevalence (95% CI)
Men 3,366 7.22 (6.39, 8.14) 1,447 12.78 (11.16, 14.61) 3,369 4.45 (3.80, 5.20) 1,446 12.69 (10.81, 14.67) 1,446 40.69 (10.04, 78.86)
Women 4,475 0.54 (0.36, 0.80) 1,825 2.19 (1.61,2.97) 4,475 0.49 (0.32, 0.75) 1,824 0.94 (0.43, 1.61) 1,824 4.73 (1.30, 9.11)
Total 7,841 3.40 (3.03, 3.83) 3,272 6.88 (6.06, 7.80) 7,844 2.19 (1.89, 2.54) 3,270 6.14 (5.17, 7.14) 3,270 28.87 (10.45, 43.74)

LCLL, latent class log-linear; CI, confidence interval.

1 95% CIs calculated using non-parametric bootstrapping with 500 iterations.

  • 1. Berzofsky ME, Biemer P, Kalsbeek W. A brief history of classification error models; 2008 [cited 2016 May 11]. Available from: http://www.amstat.org/sections/srms/proceedings/y2008/files/302416.pdf.
  • 2. Kasprzyk D. Measurement error in household surveys: sources and measurement. In: Department of Economic and Social Affairs Statistics Division. Household sample surveys in developing and transition countries. New York: United Nations; 2005. p 171-198.
  • 3. Berzofsky ME, Biemer PP, Kalsbeek WD. Local dependence in latent class analysis of rare and sensitive events. Sociol Methods Res 2014;43:137-170.ArticlePubMed
  • 4. Biemer PP, Trewin D. A review of measurement error effects on the analysis of survey data. In: Lyberg L, Biemer P, Collins M, De Leeuw E, Dippo C, Schwarz N, et al. Survey measurement and process quality. New York: Wiley; 1997. p 601-632.
  • 5. Gustafson P, Greenland S. Misclassificatio. In: Ahrens W, Pigeot I, eds. Handbook of epidemiology. New York: Springer; 2014. p 639-658.
  • 6. Lazarsfeld PF, Henry NW. Latent structure analysis. New York: Houghton Mifflin; 1968.
  • 7. Biemer PP, Wiesen C. Measurement error evaluation of self-reported druguse: a latent class analysis of the US National Household Survey on Drug Abuse. J R Stat Soc Ser A Stat Soc 2002;165:97-119.Article
  • 8. Spencer BD. When Do latent class models overstate accuracy for binary classifiers? With applications to jury accuracy, survey response error, and diagnostic error; 2009 [cited 2016 May 20]. Available from: http://www.ipr.northwestern.edu/publications/docs/workingpapers/2008/IPR-WP-08-10.pdf.
  • 9. Biemer PP. Latent class analysis of survey error. Hoboken: Wiley; 2011.
  • 10. Agresti A. Categorical data analysis. 2nd ed. New York: John Wiley & Sons; 2002. p 721.
  • 11. Brenner H. Use and limitations of dual measurements in correcting for nondifferential exposure misclassification. Epidemiology 1992;3:216-222.ArticlePubMed
  • 12. Walter SD, Irwig LM. Estimation of test error rates, disease prevalence and relative risk from misclassified data: a review. J Clin Epidemiol 1988;41:923-937.ArticlePubMed
  • 13. Rahimi-Movaghar A, Sharif V, Motevalian SA, Amin-Esmaeili M, Hajebi A, Radgoodarzi R, et al. Iranian Mental Health Survey (1389- 90). [cited 2016 May 30]. Available from: http://ketab.ir/modules.php?name=News&op=pirbook&bcode=2005339 (Persian).
  • 14. Farhoudian A, Sadeghi M, Khoddami Vishteh HR, Moazen B, Fekri M, Rahimi Movaghar A. Component analysis of Iranian crack; a newly abused narcotic substance in Iran. Iran J Pharm Res 2014;13:337-344.PubMedPMC
  • 15. Lin TH, Dayton CM. Model selection information criteria for nonnested latent class models. J Educ Behav Stat 1997;22:249-264.Article
  • 16. Dayton CM, Macready GB. A scaling model with response errors and intrinsically unscalable respondents. Psychometrika 1980;45:343-356.Article
  • 17. Goodman LA. Exploratory latent structure analysis using both identifiable and unidentifiable models. Biometrika 1974;61:215-231.Article
  • 18. Vermunt JK. Log-linear models for event histories. London: SAGE; 1997.
  • 19. R Development Core Team. R: a language and environment for statistical computing; 2015 [cited 2016 May 20]. Available from: https://www.r-project.org/.
  • 20. Duffy D. Package ‘gllm’: generalised log-linear model; 2015 [cited 2016 May 20]. Available from: https://cran.r-project.org/web/packages/gllm/gllm.pdf.
  • 21. Tourangeau R, Yan T. Sensitive questions in surveys. Psychol Bull 2007;133:859-883.ArticlePubMed
  • 22. Hui SL, Walter SD. Estimating the error rates of diagnostic tests. Biometrics 1980;36:167-171.ArticlePubMed
Appendix 1.
Definition of Indicators A, B and C of any illicit drug use in the past 12 months in the Iranian Mental Health Survey (IranMHS) data
epih-38-e2016013-app1.pdf
Appendix 2.
R software’s codes of latent class analysis for correcting measurement error while estimating prevalence of any illicit drug use in IranMHS (Model [7]):
epih-38-e2016013-app2.pdf
Appendix 3.
The reason of replacing BIC with “BIC + [2*ln(likelihood of saturated model)]” in Table 2
epih-38-e2016013-app3.pdf

Figure & Data

References

    Citations

    Citations to this article as recorded by  

      Figure
      • 0
      • 1
      Assessing measurement error in surveys using latent class analysis: application to self-reported illicit drug use in data from the Iranian Mental Health Survey
      Image Image
      Figure 1. The local independence assumption. ε, measurement error.
      Figure 2. Types of violation of the local independence assumption. (A) Behaviorally correlated error, (B) bivocality, and (C) latent heterogeneity. ε, measurement error.

      Figure 1.

      Figure 2.

      Assessing measurement error in surveys using latent class analysis: application to self-reported illicit drug use in data from the Iranian Mental Health Survey
      Indicator A Indicator C
      		 Total
      Yes No
      Yes Indicator B Yes 44 (37.6) 64 (54.7) 108 (92.3)
      No 1 (0.9) 8 (6.8) 9 (7.7)
      Total 45 (38.5) 72 (61.5) 117 (100)
      No Indicator B Yes 3 (0.1) 114 (3.6) 117 (3.7)
      No 18 (0.6) 3,018 (95.7) 3,036 (96.3)
      Total 21 (0.7) 3,132 (99.3) 3,153 (100)
      Total Indicator B Yes 47 (1.4) 178 (5.4) 225 (6.9)
      No 19 (0.6) 3,026 (92.5) 3,045 (93.1)
      Total 66 (2.0) 3,204 (98.0) 3,270 (100)
      Model Degrees of freedom No. of parameters Deviance1 p-value of likelihood ratio test BIC + [2*ln (likelihood of saturated model)]2 Prevalence (adjusted for classification error, %)
      Model 0 (AY, BY, GY) 0 8 1.70 0.99 66.44 6.14
      Model 1 (AY, BY, CY, GY) 6 10 50.45 <0.001 131.38 5.56
      Model 2: same as model 1 + (AB) 5 11 40.92 0.006 129.94 7.31
      Model 3: same as model 1 +(BC) 5 11 50.37 <0.001 139.39 5.52
      Model 4: same as model 1 + (AC) 5 11 19.90 0.53 108.92 6.18
      Model 5: same as model 1 + (AC, BC) 4 12 15.77 0.73 112.88 6.23
      Model 6: same as model 1 +(AB, BC) 4 12 38.84 0.007 135.95 7.98
      Model 7: same as model 1 +(AC, AB) 4 12 7.43 1.00 104.54 28.87
      Model 8: same as model 1 +(AC, BC, AB) 3 13 3.77 1.00 108.98 42.17
      Model 9: same as model 1 +(AG, BG, CG) 3 13 9.22 0.97 114.42 3.55
      Model 10: same as model 9+(AC, AB) 1 15 20.37 0.25 141.76 49.99
      Indicator By LCLL model with 2 indicators (model 0)
      		 By LCLL model with 3 indicators (model 7)
      Sensitivity (95% CI) Specificity (95% CI) Sensitivity (95% CI) Specificity (95% CI)
      A 58.29 (49.63, 67.53) 100.00 (reference) 12.39 (7.65, 34.45) 100.00 (reference)
      B 92.32 (87.13, 96.82) 98.70 (98.01,99.38) 20.84 (13.57, 54.89) 98.79 (98.13, 99.40)
      C - - 6.77 (4.03, 18.43) 99.91 (99.67, 100.00)
      Gender Indicator A
      		 Indicator B
      		 Indicator C
      		 LCLL (2-indicator)1
      		 LCLL (3-indicator)1
      n Prevalence (95% CI) n Prevalence (95% CI) n Prevalence (95% CI) n Prevalence (95% CI) n Prevalence (95% CI)
      Men 3,366 7.22 (6.39, 8.14) 1,447 12.78 (11.16, 14.61) 3,369 4.45 (3.80, 5.20) 1,446 12.69 (10.81, 14.67) 1,446 40.69 (10.04, 78.86)
      Women 4,475 0.54 (0.36, 0.80) 1,825 2.19 (1.61,2.97) 4,475 0.49 (0.32, 0.75) 1,824 0.94 (0.43, 1.61) 1,824 4.73 (1.30, 9.11)
      Total 7,841 3.40 (3.03, 3.83) 3,272 6.88 (6.06, 7.80) 7,844 2.19 (1.89, 2.54) 3,270 6.14 (5.17, 7.14) 3,270 28.87 (10.45, 43.74)
      Table 1. Cross-tabulation of the three indicators of illicit drug use in the past 12 months

      Values are presented as number (%).

      Table 2. Characteristics of alternative latent class log-linear models applied to the IranMHS data regarding illicit drug use

      IranMHS, Iranian Mental Health Survey; BIC, Bayesian information criterion.

      -2*(ln[likelihood of current model] – ln[likelihood of saturated model]).

      The reason for replacing BIC with “BIC [2*ln(likelihood of saturated model)]” is explained in Appendix 3.

      Table 3. Estimated sensitivity and specificity (%) of indicators of illicit drug use in the past 12 months

      F195% CIs calculated using non-parametric bootstrapping with 500 iterations.

      LCLL, latent class log-linear; CI, confidence interval.

      Table 4. Comparison of prevalence (%) estimates using indicators A, B, C and the LCLL models with two and three indicators for the use of any illicit drug in the past 12 months

      LCLL, latent class log-linear; CI, confidence interval.

      95% CIs calculated using non-parametric bootstrapping with 500 iterations.

      Table 1.

      Table 2.

      Table 3.

      Table 4.

      Epidemiol Health : Epidemiology and Health
      © Korean Society of Epidemiology.
      TOP