KSE
Articles
- Page Path
- HOME > Epidemiol Health > Volume 41; 2019 > Article
-
Methods
Diagnostic test accuracy: application and practice using R software -
Sung Ryul Shim1,2
, Seong-Jang Kim3,4, Jonghoo Lee5 -
Epidemiol Health 2019;41:e2019007.
DOI: https://doi.org/10.4178/epih.e2019007
Published online: March 28, 2019
1Department of Preventive Medicine, Korea University College of Medicine, Seoul, Korea
2Urological Biomedicine Research Institute, Soonchunhyang University Hospital, Seoul, Korea
3Department of Nuclear Medicine, Pusan National University Yangsan Hospital, Pusan National University School of Medicine, Yangsan, Korea
4BioMedical Research Institute for Convergence of Biomedical Science and Technology, Pusan National University Yangsan Hospital, Yangsan, Korea
5Department of Internal Medicine, Jeju National University Hospital, Jeju National University School of Medicine, Jeju, Korea
- Correspondence: Sung Ryul Shim Department of Preventive Medicine, Korea University College of Medicine, 145 Anam-ro, Seongbuk-gu, Seoul 02841, Korea E-mail: sungryul.shim@gmail.com
• Received: March 14, 2019 • Accepted: March 28, 2019
©2019, Korean Society of Epidemiology
This is an open-access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
- The objective of this paper is to describe general approaches of diagnostic test accuracy (DTA) that are available for the quantitative synthesis of data using R software. We conduct a DTA that summarizes statistics for univariate analysis and bivariate analysis. The package commands of R software were “metaprop” and “metabin” for sensitivity, specificity, and diagnostic odds ratio; forest for forest plot; reitsma of “mada” for a summarized receiver-operating characteristic (ROC) curve; and “metareg” for meta-regression analysis. The estimated total effect sizes, test for heterogeneity and moderator effect, and a summarized ROC curve are reported using R software. In particular, we focus on how to calculate the effect sizes of target studies in DTA. This study focuses on the practical methods of DTA rather than theoretical concepts for researchers whose fields of study were non-statistics related. By performing this study, we hope that many researchers will use R software to determine the DTA more easily, and that there will be greater interest in related research.
- General pairwise meta-analysis calculates the effect size, such as relative risk and odds ratio (OR) for binary data and the mean difference for continuous data. By contrast, the diagnostic test accuracy (DTA) simultaneously combines two effect sizes, such as the sensitivity and specificity or positive predictive value and negative predictive value [1-3].
- Therefore, DTA is more complex than pairwise meta-analysis, which has one result value. The expansion to multivariate analysis with more than two results inevitably leads to the introduction of the multi-layer concept, which requires some degree of mathematical understanding as well as an ability to use statistical programs.
- This study focuses on the procedures involved in running the R software (Supplementary Material 1) as well as the concepts of producing summary statistics, which need to be understood for DTA.
- In this study, the previous meta-analysis studies performed by the authors [1-3] are reviewed using R software. Furthermore, this study requires prior knowledge about the meta-analysis of diagnostic tests because it first deals with the types and changes of the effect size to calculate the summary statistics for DTA.
INTRODUCTION
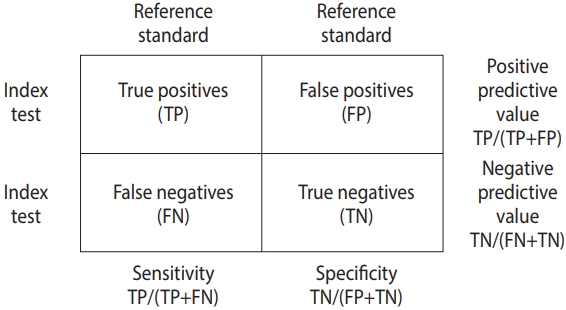
- The data for DTA assumes a 2×2 table form in which the row cells are distinguished by the presence or absence of a test, and the column cells are distinguished by the presence or absence of a disease (Figure 1).
- Summary statistics for diagnostic test accuracy
- The DTA is represented by the summary statistics and summary line from four sets of basic data, namely true positive (TP), false positive (FP), false negative (FN), and true negative (TN). Representative summary statistics are the sensitivity, specificity, diagnostic odds ratio (DOR), and forest plot, and an example summary curve is the summary receiver operating characteristic (SROC) curve (Table 1).
- Diagnostic test accuracy model
- To calculate the summary statistics for the DTA, an appropriate model should be selected, as with pairwise meta-analysis. Models that simultaneously consider the sensitivity and specificity include the Moses–Littenberg SROC model [4,5], bivariate model [6], and hierarchical SROC (HSROC) model [7].
- The Moses–Littenberg model is a simple model that was created in the early stage to determine the DTA, and it estimates the SROC using simple linear regression. This is similar to the fixed-effect model in pairwise meta-analysis, and cannot estimate the heterogeneity between studies. Furthermore, this model cannot distinguish between within-study and between-study variations in all variations, and can perform limited analysis because it only provides the SORC curve without parameter estimates, standard deviation, or confidence intervals (CIs).
- To overcome the disadvantages of the Moses–Littenberg model, the bivariate model and HSROC model were developed based on the hierarchical model. These two models provide the same value mathematically when there is no covariate [8,9]. This is similar to the random-effect model in pairwise meta-analysis. Both models can estimate the within-study and between-study variation of studies, that is, the heterogeneity.
- The bivariate model assumes a binominal distribution that directly models the sensitivity and specificity for within-study variations, while assuming a bivariate normal distribution for between-study variation. However, the HSROC model assumes a binominal distribution for within-study variations, while assuming a hierarchical distribution for parameters included in the logistic model by applying the logistic regression model to determine the probability of a binominal distribution for between-study variation.
- The R “mada” package reitsma model, which we will practice in this book, calculates the summary statistics and estimates the SROC curve using the bivariate model by default.
- Calculation of effect size
- Examine the sensitivity and specificity in Table 1.
- The sensitivity is TP/(TP+FN), and the specificity is TN/(TN+FP), which are proportion-type data.
- For these proportion-type data, logit-transformed data are used more often than raw data. The logit transformation is a method of adjusting the data distribution according to statistical assumptions. The proportion-type data are limited between the lower and upper limits of 0 and 1, respectively. To convert these data to make them appropriate for the assumptions of statistics, their upper and lower limits should be released by performing multiplication and log transformations, respectively. This is called logit transformation.
- Upon completion of the calculation of the summary statistics for DTA, they are reverted to their original values for interpretation. In the practice using R, we will calculate the logit-transformed sensitivity and specificity using the “metaprop” function of the “meta” package and then revert them to their original values to interpret them. Thus, we should understand why the effect size is transformed.
UNDERSTANDING DIAGNOSTIC TEST ACCURACY
- Figure 2 shows the flow of the DTA. First, when coding the data, we must change the variable name appropriately for the corresponding function. After selecting a meta-analysis model (fixed or random), the total effect size is presented, the heterogeneity is verified, and the publication bias is then verified and reported.
- The “mada” package is required to analyze the DTA in R. After “mada” is installed, you will be promoted to install “mvtnorm,” “ellipse,” and “mvmeta.” Thus, you should install them in advance as follows:
- ·install.packages(“mada”)
- ·install.packages(“mvtnorm”)
- ·install.packages(“ellipse”)
- ·install.packages(“mvmeta”)
- In addition, you should install the “meta,” “metafor,” and “rmeta” packages for general pairwise intervention meta-analysis in R as follows:
- ·install.packages(“meta”)
- ·install.packages(“metafor”)
- ·install.packaqes(“rmeta”)
- The main explanations are applicable to the “mada” and “meta” packages. For detailed explanations about the “mada” package, refer to detailed codes, documents, and references for the package [10].
- We mark R commands with a dot (‘·’) in front of them, to distinguish them from the main text. When long commands are extended to the next line, there is no dot at the beginning of the next line. Thus, when you enter the command in the R software, you must type them without the dot (‘·’) in front of them.
- Data coding and loading
- As an example of the DTA, the urine sample measuring the albumin concentration method (Table 2) was selected from among the test methods for microalbuminuria in diabetes patients [2,3,11]. Subgroup (g) 1 consists of Western European counties, and 0 consists of countries other than Western European countries.
- Load the example file from the working folder with the following command. Note that R prefers comma-separated values (csv) file format. Thus, you should save Table 2 as “dta_shim.csv” in the specified working folder.
- ·dta_shim <- read.csv (“dta_shim.csv”, header=TRUE)
- read.csv is a function for loading a csv file. The above command means to load the file “dta_shim.csv” and use the first variable name (header=TRUE). This loaded file is saved as “dta_shim” in the R memory. To confirm this, enter the specified data in the View() function.
- Summary statistics
- The “mada” package, which is a bivariate model for calculating the summary statistics for the DTA, does not provide the total effect sizes of summary statistics (sensitivity, specificity, and DOR) and only provides the effect size of individual studies as a forest plot, which is inconvenient.
- Therefore, it is more natural to check the value of each summary statistic by performing univariate analysis using the “meta” package first, and then to present an SROC curve using the “mada” package.
- Univariate analysis
- Calculate the sensitivity, specificity, and DOR and plot them using the univariate analysis model.
- Load the meta package to perform meta-analysis:
- ·library(meta)
- The “meta” package includes many functions. Among them, the “metaprop” function calculates the total effect size using the number of events (event) and the number of samples (n) from proportion-type data.
- · sensitivity_logit <- metaprop(dta_shim$TP, dta_shim$TP+ dta_shim$FN, comb.fixed=FALSE, comb.random=TRUE, sm=“PLOGIT”, method.ci=“CP”, studlab=dta_shim$id, byvar=dta_shim$g)
- ·print(sensitivity_logit, digits=3)
- In sensitivity analysis, the number of events is TP and the number of samples is TP+FN. The variables of these data in R can be indicated by using the symbol ‘$’ (for example, write “dta_shim$TP” to indicate the TP variable of the dta_shim data). After sequentially entering the number of events (dta_shim$TP) and the number of samples (dta_shim$TP+dta_shim$FN) in the metaprop function, input other optional arguments at the end.
- To calculate the effect size from proportion-type data, the method of reverting after logit transformation was used. Besides, you can enter sm=“PRAW” to use the raw data without transformation, or sm=“PLN” to find the reverted value after log transformation.
- For consistency with the assumptions of the statistic model, and to consider the symmetricity and distribution of data, it is desirable to transform proportion-type data (log transformation or logit transformation) as they produce conservative results. However, many previous studies and statistical models have broadened the operation scope of researchers. Thus, it is necessary to find and use an appropriate method for the research results.
- Even if data transformation is performed, the “metaprop” function automatically reverts and shows the total effect size that can be interpreted.
- Furthermore, there are several methods for calculating the confidence interval, but the default Clopper–Pearson method is recommended as it is not too complex (method.ci=“CP”).
- The random effect model was used, and comb.fixed=FALSE and comb.random=TRUE are also entered. The desired model can be selected by using FALSE or TRUE.
- Studlab=study indicates the name of individual studies. To show the result by subgroup, enter “byvar=g” where g is the variable name representing the subgroup. The results obtained when using the “metaprop” function are assigned to sensitivity_logit, and the result is shown in Figure 3.
- The results from sensitivity_logit in Figure 3 are examined below one-by-one.
- ① Shows the total effect size of all nine studies. The proportion of the random effect model was 0.841 (95% CI, 0.788 to 0.882).
- ② Shows the result corresponding to the subgroup. The random model shows slight differences in sensitivity according to the subgroup (0 vs. 1). Based on the random effect model, the proportion is 0.816 for Western Europe countries and 0.855 for other countries. These values need to be tested using meta regression analysis according to country group later.
- ③ Shows the heterogeneity of all studies. The Higgins’ I2 of the heterogeneity is determined by subtracting the number of degrees of freedom from the Cochrane Q statistics, and then again dividing the resulting value by the Cochrane Q statistics. Thus, it quantifies the heterogeneity in a consistent manner. Values between 0% and 40% indicate that the heterogeneity may not be important; values between 30% and 60% indicate moderate heterogeneity; values between 50% and 90% indicate substantial heterogeneity; and values between 75% and 100% indicate considerable heterogeneity. The p-value of the Cochrane Q statistics is 0.1, which is a somewhat wide range of significance [3].
- In this sensitivity analysis, the Higgins’ I2 is 32.5% and the Cochrane Q statistics p-value is 0.158, which suggest weak heterogeneity.
- In addition, the calculation process for the results is revealed at the bottom of Figure 3. The inverse variance method is a basic meta-analysis method, and uses the inverse variance of the relevant study when calculating the weights of individual studies. The DerSimonian-Laird estimator indicates that the tau value was used when calculating the between-study variance.
- Furthermore, logit transformation and Clopper–Pearson method were used.
■ Forest plot
· forest(sensitivity_logit, digits=3, rightcols=c(“effect”, “ci”), xlab=“Sensitivity”)
- Enter the corresponding meta-analysis model (sensitivity_logit) in the forest function. Then, various options can be entered to facilitate identification. “digits=3” indicates that it shows only down to three decimal places, and “rightcols=c(“effect,” “ci”))” indicates that it shows the effect size and CI while omitting only the weight at the right side of the forest plot.
- In addition, the addition of colors or the addition/removal of certain information is possible at one’s discretion. You can learn more details by practicing the meta package.
- The forest plot provides the same information as the above-mentioned total effect size. Furthermore, within-study and between-study variation can be easily identified by the graphic representation of the effect size of individual studies.
- For example, it can be seen that Gansevoort, Ng, Wiegmann, and Ahn have large within-study variations, and Wiegmann and Incerti have large between-study variations.
· specificity_logit <- metaprop(dta_shim$TN, dta_shim$TN+ dta_shim$FP, comb.fixed=FALSE, comb.random=TRUE, sm=“PLOGIT”, method.ci=“CP”, studlab=dta_shim$id, byvar=dta_shim$g)
·print(specificity_logit, digits=3)
- In the specificity analysis, the number of events is TN and the number of samples is TN+FP. After sequentially entering the number of events (dta_shim$TN) and the number of samples (dta_shim$TN+dta_shim$FP) in the metaprop function, input other optional arguments, respectively. The explanation after this is identical to that of the sensitivity analysis.
- We will examine the results of specificity_logit one-by-one.
- The total effect size of all nine studies is shown. The proportion of the random effect model was 0.861 (95% CI, 0.794 to 0.909).
- The random model shows almost no difference in terms of the effect size between the subgroup (0 vs. 1). The Higgins’ I2 in this specificity analysis is 78.3%, and the p-value of Cochrane Q statistics is <0.0001, which indicates the existence of heterogeneity.
■ Forest plot
· forest(specificity_logit, digits=3, rightcols=c(“effect”, “ci”), xlab=“Specificity”)
- The explanation for this command is the same as that for the sensitivity analysis.
- The “meta” package includes several functions. Among them, the “metabin” function calculates the total effect size from binary data when there exist all of the raw data. The respective sensitivity and specificity are proportion-type data, but the DOR of the 2×2 format is binary data.
- · DOR_model <- metabin(TP,TP+FP,FN,FN+TN, sm=”OR”, comb.fixed=FALSE,comb.random=TRUE, method=“Inverse,” id, byvar=g, data=dta_shim)
- ·print(DOR_model)
- For binary data, enter TP, TP+FP, FN, and FN+TN in this order.
- Write OR for effect size (sm=“OR”) and use the general inverse variance method for weights of individual studies (method=“Inverse”).
- To set the random effect model considering the between-study variations, additionally enter “comb.fixed=FALSE” and “comb.random=TRUE.”
- “id” indicates the name of the individual study, and “data=dta_shim” specifies the data “dta_shim” loaded to the R memory. To show the result for each g, enter “byvar=g,” where g is the variable name for the g. The results of the metabin function are assigned to the DOR model.
■ Forest plot
· forest(DOR_model, digits=3, rightcols=c(“effect”, “ci”), xlab =“Diagnostic Odds Ratio”)
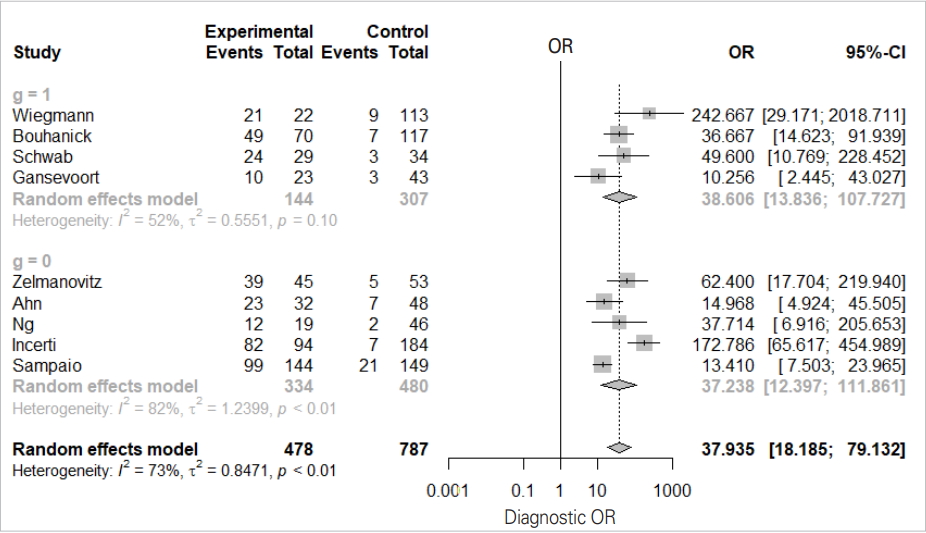
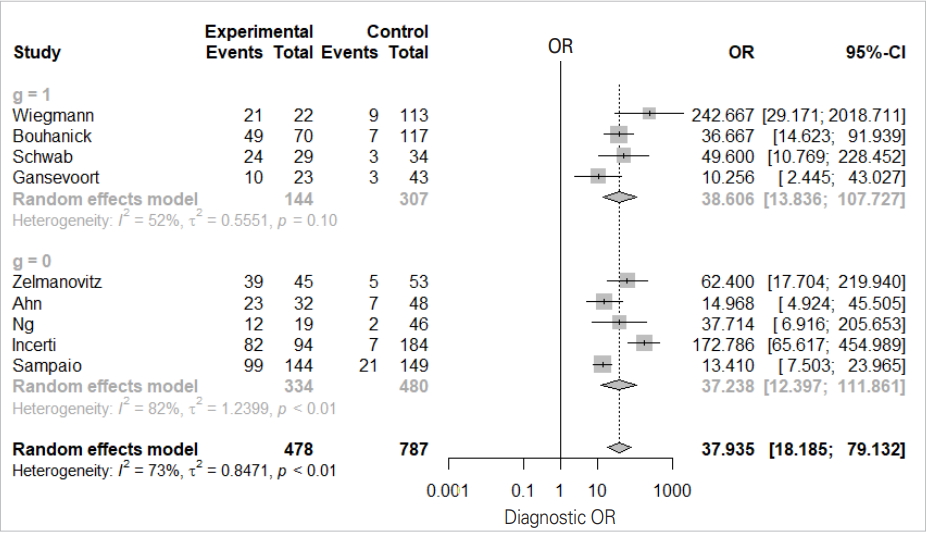
- We will examine the results of the DOR_model in Figure 4 one-by-one.
- The total effect sizes of all nine studies are shown. The OR of the random effect model is 37.935 (95% CI, 18.186 to 79.132) and p-value <0.0001. In this diagnosis test, the OR for the positive result among persons with a disease was approximately 38 times higher than the OR for positive results among persons with no disease.
- It appears that the random model has almost no difference according to subgroup (0 vs. 1).
- The Higgins’ I2 of all studies is 72.7%, and the p-value of the Cochrane Q statistics is 0.0003, indicating that there is heterogeneity.
- Bivariate analysis
- The “mada” package for bivariate analysis does not directly present the sensitivity, specificity, and DOR as in Meta-DiSc or STATA, which are other DTA applications. Thus, to show the combined overall statistics with “mada” package you should check the source code and calculate it manually.
- Therefore, in this study, the summary statistics were analyzed separately for sensitivity, specificity, and DOR by performing univariate analysis. In the following bivariate analysis, only the SROC curve is estimated using the “mada” package.
- Before loading the “mada” package, the “meta” package that was used before should be unloaded, because “mada” and “meta” both use the “forest” function, which may not be executed if it is called simultaneously by both packages.
- ·detach(package:meta)
- Load the “mada” package for bivariate analysis:
- ·library(mada)
- To see the forest plots of univariate analysis for sensitivity, specificity, and DOR using the “mada” package, enter the following commands:
- · forest(madad(dta_shim), type=“sens”, xlab=“Sensitivity”, snames=dta_shim$id)
- · forest(madad(dta_shim), type=“spec”, xlab=“Specificity”, snames=dta_shim$id)
- ·forest(madauni(dta_shim))
- These plots are the same as those obtained in the univariate analysis, and are not recommended because they do not show the overall effect size of the summary statistics.
- In the “mada” package, use the reitsma function, which is appropriate for a bivariate model.
- ·fit <- reitsma(dta_shim, correction.control=“single”)
- ·summary(fit)
- Enter the dta_shim data in the reitsma function. It becomes impossible to calculate if there is ‘0’ in a data cell. To prevent this, you can enter 0.5 in all cells of every study (correction.control= “all”), or correct only the cell of the corresponding study (horizontal) (correction.control=“single”). In the options, you can adjust it to a random value such as ‘correction=0.5,’ where 0.5 is the default value. For models using the reitsma function, ‘fit’ is assigned.
- In addition, you can refer to the area under the curve (AUC), which is 0.906, in the middle of the console window and the values corresponding to the HSROC model.
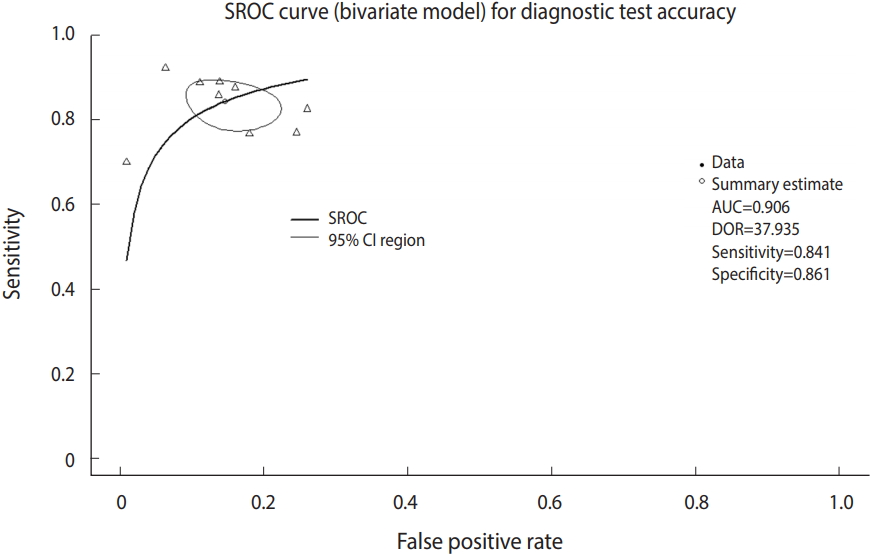
- Now, we will draw the SROC curve (Figure 5). The graphs will be drawn in the order of commands by overlapping because the first SROC curve remains in the memory.
- · plot(fit, sroclwd=2, xlim=c(0,1), ylim=c(0,1), main=“SROC curve (bivariate model) for Diagnostic Test Accuracy”)
- “plot” is a graph drawing function. Enter the set model fit. “sroclwd=2” indicates the thickness of the SROC curve. Adjust the units of the x and y axes by adjusting xlim and ylim, respectively. The current graph shows the range from a minimum of 0 to a maximum of 1.
- ·points(fpr(dta_shim), sens(dta_shim), pch=2)
- Enter the individual study in points. fpr() and sens() respectively indicate the false positive rate and sensitivity of individual studies in the corresponding data. pch=2 indicates a triangle shape. You can choose from among various shapes: rectangle (0), circle (1), triangle (2), cross (3), scissors (4), rhombus (5), inverted triangle (6), star (8), and black dot (20). The black dot (20) appears to have the best discrimination (Figure 5).
- ·legend(“bottomleft,” c(“SROC,” “95% CI region”), lwd=c(2,1))
- There is an annotation for each curve at the left bottom of the SROC curve.
- Heterogeneity review
- Once the summary statistics and the SROC summary line are presented, we have the major components of the DTA. Then, if there is any significant heterogeneity of study, researchers should verify it and report the heterogeneity factors. The basic assumption of the SROC curve is that the shape of the ROC curve is identical in all studies. However, this basic assumption is not met if there is heterogeneity between studies. There are many causes of this heterogeneity such as chance, difference in cut-off value, difference in study design, prevalence, research environment, and the demographic factors of the sample population [3].
- The DTA presents various methods for diagnosing the heterogeneity [3].
- First, the asymmetry of the SROC curve may be a cause of heterogeneity.
- Second, heterogeneity may be suspected if the degree of scattering or variation of individual studies in the SROC curve is large.
- Third, heterogeneity may be suspected if the between-study variation is greater than the within-study variation in the forest plot (sensitivity, specificity, DOR).
- Fourth, heterogeneity may be suspected if the correlation coefficient of sensitivity and specificity is larger than zero.
- The first to third factors only depend on visual distinction, so only the overall outline can be seen.
- The symmetry of the SROC curve indicates the agreement of the models of the divided SROC curves when the SROC curve is divided by a random line from the top of the y-axis to the right bottom of the x-axis. In other words, when the SROC curve is symmetrical and the inflection point is drawn to the top left corner and sharply turned, the area AUC of the SROC curve increases and the Youden’s J index (J=sensitivity+specificity-1) becomes high, which indicate a good DTA.
- In visual verification, the SROC curve in this example does not appear to have a high symmetry, and the degree of scattering of individual studies also does not appear to be large.
- According to the within-study and between-study variation in the forest plot (Figure 4), the between-study variation does not appear to be large.
■ Sensitivity and specificity correlation coefficient
Finally, to examine the correlation coefficient of sensitivity and specificity, additional variables are created for the current data as follows:
· dta_shim$sn <- dta_shim$TP/(dta_shim$TP+dta_shim$FN)
·dta_shim$sp <- dta_shim$TN/(dta_shim$FP+dta_shim$TN)
·dta_shim$logitsn <- log(dta_shim$sn/(1-dta_shim$sn))
·dta_shim$logitsp <- log(dta_shim$sp/(1-dta_shim$sp))
- First, the sensitivity (dta_shim$sn) and specificity of each study are determined using the equations. Then, the sensitivity and specificity, which are proportion data, are logit-transformed to meet the distribution assumption. Then, the variables are checked to determine whether they have been created properly.
- ·View(dta_shim)
- Once the variables are logit-transformed, the correlation coefficient of the sensitivity and specificity is obtained as follows:
- ·cor(dta_shim$logitsn, dta_shim$logitsp)
- The correlation coefficient function is “cor”. When the logit-transformed sensitivity and specificity are entered in this function, a correlation coefficient of -0.227 is obtained.
- If the sensitivity and specificity are mutually equal and have a normal symmetric distribution, they show a trade-off relationship. The two are balanced against each other, and when one of them is lowered, the other one is raised. Therefore, the sizes of these two measurements differ in opposite directions depending on the cut-off value in the diagnostic test, and hence, these two values inevitably have a negative correlation.
- The correlation coefficient in this example is a negative value, indicating a low heterogeneity.
■ Meta regression analysis
The “mada” package does not provide functions for the meta regression analysis of the DTA. Therefore, the statistical significance of the moderating variable subgroup (Western European countries vs. other countries) is verified by performing meta regression analysis with the DOR as the effect size.
·library(meta)
·metareg(DOR_model, g, method.tau=“REML,” digits=3)
- Load the “meta” package into the memory again because it was unloaded before the “mada” package was loaded.
- Then, enter the DOR meta-analysis model (DOR_model) and the moderating variable g into the meta regression analysis function metareg. Next, determine the between-study variation of restricted maximum-likelihood estimator, and check the value to only three decimal places.
- The meta regression analysis result confirmed that the p-value of the moderating variable g was 0.922, indicating statistical insignificance.
DIAGNOSTIC TEST ACCURACY USING THE “mada” AND “meta” PACKAGES OF R
Sensitivity
Specificity
Diagnostic odds ratio
Diagnostic test accuracy summary line (summary receiver operating characteristic curve)
- This study summarized statistical theory and focused on the actual performance of meta-analysis so that it is easily understandable to general researchers who do not have majors in statistics. In other words, this study aimed to allow general researchers to adequately use already developed statistical methods in their respective fields of study to interpret the results.
- Performing an analysis to determine the DTA in R software can be a complex task because one needs to use various packages. Therefore, we recommend that researchers learn the analysis method using STATA and Meta-DiSc applications as well, which can be operated as a single package.
- Researchers who desire to perform an analysis of the DTA should establish the concepts of summary statistics and summary line.
- We hope that this study will help domestic researchers perform meta-analysis more easily, and that it will encourage related research.
CONCLUSION
SUPPLEMENTARY MATERIALS
ACKNOWLEDGEMENTS
Figure 2.Flow chart of diagnostic test accuracy (DTA) using R “mada” & “meta” package. TP, true positive; FP, false positive; FN, false negative; TN, true negative; DOR, diagnostic odds ratio; SROC, summary receiver operating characteristic.
Figure 4.Univariate analysis: diagnostic odds ratio. OR, odds ratio; CI, confidence interval; g, subgroup.
Figure 5.Summary receiver operating characteristic (SROC) curve (bivariate model) for diagnostic test accuracy. CI, confidence interval; AUC, area under the curve; DOR, diagnostic odds ratio.
Table 1.Diagnostic test accuracy summary statistics [2]
Table 2.Sample data for diagnostic test accuracy [2]
- 1. Hwang SD, Shim SR. Meta-analysis: from forest plot to network meta-analysis. Seoul: Hannarae; 2018. p 224-246 (Korean).
- 2. Shim SR. Diagnostic test accuracy using R & Meta-DiSc software. Gwacheon: SDB Lab; 2019. (Korean).
- 3. Shim SR, Shin IS, Bae JM. Meta-analysis of diagnostic tests accuracy using STATA software. J Health Info Stat 2015;40:190-199 (Korean).
- 4. Moses LE, Shapiro D, Littenberg B. Combining independent studies of a diagnostic test into a summary ROC curve: data analytic approaches and some additional considerations. Stat Med 1993;12:1293-1316.ArticlePubMed
- 5. Littenberg B, Moses LE. Estimating diagnostic accuracy from multiple conflicting reports: a new meta analytic method. Med Decis Making 1993;13:313-321.ArticlePubMed
- 6. Reitsma JB, Glas AS, Rutjes AW, Scholten RJ, Bossuyt PM, Zwinderman AH. Bivariate analysis of sensitivity and specificity produces informative summary measures in diagnostic reviews. J Clin Epidemiol 2005;58:982-990.ArticlePubMed
- 7. Rutter CM, Gatsonis CA. A hierarchical regression approach to meta-analysis of diagnostic test accuracy evaluations. Stat Med 2001;20:2865-2884.ArticlePubMed
- 8. Arends LR, Hamza TH, van Houwelingen JC, Heijenbrok-Kal MH, Hunink MG, Stijnen T. Bivariate random effects meta-analysis of ROC curves. Med Decis Making 2008;28:621-638.ArticlePubMed
- 9. Harbord RM, Deeks JJ, Egger M, Whiting P, Sterne JA. A unification of models for meta-analysis of diagnostic accuracy studies. Biostatistics 2007;8:239-251.ArticlePubMedPDF
- 10. Comprehensive R Archive Network. mada: meta-analysis of diagnostic accuracy. [cited 2019 May 8]. Available from: https://cran.r-project.org/web/packages/mada/index.html.Article
- 11. Wu HY, Peng YS, Chiang CK, Huang JW, Hung KY, Wu KD, et al. Diagnostic performance of random urine samples using albumin concentration vs ratio of albumin to creatinine for microalbuminuria screening in patients with diabetes mellitus: a systematic review and meta-analysis. JAMA Intern Med 2014;174:1108-1115.ArticlePubMed
REFERENCES
Figure & Data
References
Citations
Citations to this article as recorded by 
- Diagnostic accuracy of artificial intelligence models in detecting osteoporosis using dental images: a systematic review and meta-analysis
Gita Khadivi, Abtin Akhtari, Farshad Sharifi, Nicolette Zargarian, Saharnaz Esmaeili, Mitra Ghazizadeh Ahsaie, Soheil Shahbazi
Osteoporosis International.2025; 36(1): 1. CrossRef - Diagnostic Performance of ASL-MRI and FDG-PET in Frontotemporal Dementia: A Systematic Review and Meta-Analysis
Richard Dagher, Parisa Arjmand, Burak Berksu Ozkara, Mahla Radmard, Mona Gad, Ali Sheikhy, Max Wintermark, Vivek Yedavalli, Haris I. Sair, Licia P. Luna
American Journal of Neuroradiology.2025; 46(2): 341. CrossRef - %diag_test: a generic SAS macro for evaluating diagnostic accuracy measures for multiple diagnostic tests
Jacques K. Muthusi, Peter W. Young, Frankline O. Mboya, Samuel M. Mwalili
BMC Medical Informatics and Decision Making.2025;[Epub] CrossRef - The Efficacy and Safety of Metastasis-directed Therapy in Patients with Prostate Cancer: A Systematic Review and Meta-analysis of Prospective Studies
Marcin Miszczyk, Pawel Rajwa, Takafumi Yanagisawa, Zuzanna Nowicka, Sung Ryul Shim, Ekaterina Laukhtina, Tatsushi Kawada, Markus von Deimling, Benjamin Pradere, Juan Gómez Rivas, Giorgio Gandaglia, Roderick C.N. van den Bergh, Gregor Goldner, Stephane Sup
European Urology.2024; 85(2): 125. CrossRef - Comparable performance of antigen‐detecting rapid test by healthcare worker‐collected and self‐collected swabs for SARS‐CoV‐2 diagnostic: A systematic review and meta‐analysis
Samuel Johnson Kurniawan, Maria Mardalena Martini Kaisar, Helen Kristin, Soegianto Ali
Reviews in Medical Virology.2024;[Epub] CrossRef - Diagnostic performance of angiography‐derived fractional flow reserve and CT‐derived fractional flow reserve: A systematic review and Bayesian network meta‐analysis
Zhongxiu Chen, Junyan Zhang, Yujia Cai, Hongsen Zhao, Duolao Wang, Chen Li, Yong He
Journal of Evidence-Based Medicine.2024; 17(1): 119. CrossRef - Advancing accuracy in breath testing for lung cancer: strategies for improving diagnostic precision in imbalanced data
Ke-Cheng Chen, Shuenn-Wen Kuo, Ruei-Hao Shie, Hsiao-Yu Yang
Respiratory Research.2024;[Epub] CrossRef - Diagnostic Accuracy of Deep Learning for the Prediction of Osteoporosis Using Plain X-rays: A Systematic Review and Meta-Analysis
Tzu-Yun Yen, Chan-Shien Ho, Yueh-Peng Chen, Yu-Cheng Pei
Diagnostics.2024; 14(2): 207. CrossRef - The diagnostic utility of heparin-binding protein among patients with bacterial infections: a systematic review and meta-analysis
Amira Mohamed Taha, Khaled Abouelmagd, Mohamed Mosad Omar, Qasi Najah, Mohammed Ali, Mohammed Tarek Hasan, Sahar A. Allam, Roua Arian, Omar El Sayed Rageh, Mohamed Abd-ElGawad
BMC Infectious Diseases.2024;[Epub] CrossRef - Comparative Study of Different Imaging Modalities for Diagnosis of Bone Metastases of Prostate Cancer
Keunyoung Kim, Mihyang Ha, Seong-Jang Kim
Clinical Nuclear Medicine.2024; 49(4): 312. CrossRef - The diagnostic performance of ultrafast MRI to differentiate benign from malignant breast lesions: a systematic review and meta-analysis
Yoav Amitai, Vivianne A. R. Freitas, Orit Golan, Rivka Kessner, Tamar Shalmon, Rina Neeman, Michal Mauda-Havakuk, Diego Mercer, Miri Sklair-Levy, Tehillah S. Menes
European Radiology.2024; 34(10): 6285. CrossRef - Clinical Presentation, Risk Factors, and Comparison of Laboratory Diagnostics for Seasonal Influenza Virus Among Cambodians From 2007 to 2020
Agus Rachmat, Gerard C Kelly, Long Khanh Tran, Nathaniel Christy, Chonthida Supaprom, Vireak Heang, Sokha Dul, Jose A Garcia-Rivera, Satharath Prom, Heng Sopheab, John S Brooks, Ian J Sutherland, Karen S Corson, Andrew G Letizia
Open Forum Infectious Diseases.2024;[Epub] CrossRef - Juvenile sex estimation using the elevation of the auricular surface: A systematic review and meta‐analysis
Maura K. Griffith, Carolyn Rando
International Journal of Osteoarchaeology.2024;[Epub] CrossRef - Prognostic nutritional index as a predictive marker for acute kidney injury in adult critical illness population: a systematic review and diagnostic test accuracy meta-analysis
Jia-Jin Chen, Tao-Han Lee, Pei-Chun Lai, Chih-Hsiang Chang, Che-Hsiung Wu, Yen-Ta Huang
Journal of Intensive Care.2024;[Epub] CrossRef - Diagnostic and prognostic value of heparin-binding protein in sepsis: A systematic review and meta-analysis
Amira Mohamed Taha, Qasi Najah, Mohamed Mosad Omar, Khaled Abouelmagd, Mohammed Ali, Mohammed Tarek Hasan, Sahar A. Allam, Yasser A. Hamam, Roua Arian, Mohamed Abd-ElGawad
Medicine.2024; 103(25): e38525. CrossRef - The conundrum of differentiating Cushing’s syndrome from non-neoplastic hypercortisolism: a systematic review and meta-analysis
José Miguel Hinojosa-Amaya, Fernando Díaz González-Colmenero, Neri Alejandro Alvarez-Villalobos, Alejandro Salcido-Montenegro, Carolina Quintanilla-Sánchez, Pablo José Moreno-Peña, Dulce María Manzanares-Gallegos, Luis Fernando Gutiérrez-Dávila, Patricia
Pituitary.2024; 27(4): 345. CrossRef - Artificial intelligence/machine learning for neuroimaging to predict hemorrhagic transformation: Systematic review/meta‐analysis
Richard Dagher, Burak Berksu Ozkara, Mert Karabacak, Samir A. Dagher, Elijah Isaac Rumbaut, Licia P. Luna, Vivek S. Yedavalli, Max Wintermark
Journal of Neuroimaging.2024; 34(5): 505. CrossRef - Diagnostic accuracy of cytology and urine methylation test in patients with non-muscle invasive bladder cancer: a systematic review and meta-analysis
Zhuoyue Yao, Tao Wang, Jingpeng Liu, Zhongbao Zhou, Yong Zhang
Frontiers in Oncology.2024;[Epub] CrossRef - Cardiac CT vs Echocardiography for Intracardiac Thrombus Detection in Ischemic Stroke
Sherief Ghozy, Michael Liu, Hassan Kobeissi, Ali Mortezaei, Melika Amoukhteh, Alzhraa S. Abbas, Adam A. Dmytriw, Ramanathan Kadirvel, Alejandro A. Rabinstein, David F. Kallmes, Deena Nasr
Neurology.2024;[Epub] CrossRef - Diagnostic yield and safety of diagnostic techniques for pulmonary lesions: systematic review, meta-analysis and network meta-analysis
Prasanth Balasubramanian, David Abia-Trujillo, Alana Barrios-Ruiz, Ana Garza-Salas, Anoop Koratala, Nikitha C. Chandra, Alejandra Yu Lee-Mateus, Gonzalo Labarca, Sebastian Fernandez-Bussy
European Respiratory Review.2024; 33(173): 240046. CrossRef - Application of machine learning for predicting lymph node metastasis in T1 colorectal cancer: a systematic review and meta-analysis
Chinock Cheong, Na Won Kim, Hye Sun Lee, Jeonghyun Kang
Langenbeck's Archives of Surgery.2024;[Epub] CrossRef - Feasibility and diagnostic accuracy of neonatal anthropometric measurements in identifying low birthweight and preterm infants in Africa: a systematic review and meta-analysis
Fitsum Weldegebriel Belay, Rekiku Fikre, Akalewold Alemayehu, Andrew Clarke, Sarah Williams, Hannah Richards, Yohannes Chanyalew Kassa, Fanuel Belayneh Bekele
BMJ Paediatrics Open.2024; 8(1): e002741. CrossRef - Diagnostic Utility of SARS-CoV-2 Nucleocapsid Antigenemia: A Meta-analysis
Gregory L Damhorst, Sydney E Martin, Eli Wilber, Hans Verkerke, Michael Goodman, Wilbur A Lam
Open Forum Infectious Diseases.2024;[Epub] CrossRef - Comparison of different diagnostic protocols for the detection of Toxocara spp. in faecal samples of cats and dogs
Deliah Tamsyn Winterfeld, Birgit Schauer, Majda Globokar, Nikola Pantchev, Susan Mouchantat, Franz Josef Conraths, Helge Kampen, Johanna Dups-Bergmann, Gereon Schares, Pavlo Maksimov
Parasites & Vectors.2024;[Epub] CrossRef - Diagnostic Accuracy and Prognostic Value of Relative Apical Sparing in Cardiac Amyloidosis ― Systematic Review and Meta-Analysis ―
Chung-Yen Lee, Yosuke Nabeshima, Tetsuji Kitano, Li-Tan Yang, Masaaki Takeuchi
Circulation Journal.2024; 89(1): 16. CrossRef - Diagnostic Accuracy of CT for the Detection of Hepatic Steatosis: A Systematic Review and Meta-Analysis
Maryam Haghshomar, Dominic Antonacci, Andrew D. Smith, Sarang Thaker, Frank H. Miller, Amir A. Borhani
Radiology.2024;[Epub] CrossRef - Ultrasound and computed tomography in differentiating between simple and complicated appendicitis in pediatric patients
Mohamad Badlis, Kamil Amari, Maya Alkheshi, Karim Alolaby, Bayan Alsaid
Pediatric Surgery International.2024;[Epub] CrossRef - Detection of Alzheimer's Disease in Neuroimages using Vision Transformers: A Systematic Review and Meta-Analysis (Preprint)
Vivens Mubonanyikuzo, Hongjie Yan, Temitope Emmanuel Komolafe, Liang Zhou, Tao Wu, Nizhuan Wang
Journal of Medical Internet Research.2024;[Epub] CrossRef - Identifying the culprit artery via 12‐lead electrocardiogram in inferior wall ST‐segment elevation myocardial infarction: A meta‐analysis
Peng Zhou, Yingying Wu, Meng Wang, Yikai Zhao, Yangjie Yu, Maieryemu Waresi, Huiyang Li, Bo Jin, Xinping Luo, Jian Li
Annals of Noninvasive Electrocardiology.2023;[Epub] CrossRef - Clinical value of alarm features for colorectal cancer: a meta-analysis
Leonardo Frazzoni, Liboria Laterza, Marina La Marca, Rocco Maurizio Zagari, Franco Radaelli, Cesare Hassan, Alessandro Repici, Antonio Facciorusso, Paraskevas Gkolfakis, Cristiano Spada, Konstantinos Triantafyllou, Franco Bazzoli, Mario Dinis-Ribeiro, Lor
Endoscopy.2023; 55(05): 458. CrossRef - CA125 for the Diagnosis of Advanced Urothelial Carcinoma of the Bladder: A Systematic Review and Meta-Analysis
Hsuan-Jen Lin, Rouh-Mei Hu, Hung-Chih Chen, Chung-Chih Lin, Chi-Yu Lee, Che-Yi Chou
Cancers.2023; 15(3): 813. CrossRef - Performance of screening tools for cervical neoplasia among women in low- and middle-income countries: A systematic review and meta-analysis
Sabrina K. Smith, Oguchi Nwosu, Alex Edwards, Meseret Zerihun, Michael H. Chung, Kara Suvada, Mohammed K. Ali, Nebiyu Dereje
PLOS Global Public Health.2023; 3(2): e0001598. CrossRef - Diagnostic accuracy of point-of-care lung ultrasound for COVID-19: a systematic review and meta-analysis
Ashley Matthies, Michael Trauer, Karl Chopra, Robert David Jarman
Emergency Medicine Journal.2023; 40(6): 407. CrossRef - Influence of seasonal and operator variations on diagnostic accuracy of lateral flow devices during the COVID-19 pandemic: a systematic review and meta-analysis
Ashwin Krishnamoorthy, Subashini Chandrapalan, Gohar JalayeriNia, Yaqza Hussain, Ayman Bannaga, Ian Io Lei, Ramesh Arasaradnam
Clinical Medicine.2023; 23(2): 144. CrossRef - Prognostic role of different findings at echocardiography in acute pulmonary embolism: a critical review and meta-analysis
Ludovica Anna Cimini, Matteo Candeloro, Magdalena Pływaczewska, Giorgio Maraziti, Marcello Di Nisio, Piotr Pruszczyk, Giancarlo Agnelli, Cecilia Becattini
ERJ Open Research.2023; 9(2): 00641-2022. CrossRef - Virotyping and genetic antimicrobial susceptibility testing of porcine ETEC/STEC strains and associated plasmid types
Nick Vereecke, Sander Van Hoorde, Daniel Sperling, Sebastiaan Theuns, Bert Devriendt, Eric Cox
Frontiers in Microbiology.2023;[Epub] CrossRef - The Diagnostic Power of Circulating miR-1246 in Screening Cancer: An Updated Meta-analysis
Khanh Quang Huynh, Anh Tuan Le, Thang Thanh Phan, Toan Trong Ho, Suong Phuoc Pho, Hang Thuy Nguyen, Binh Thanh Le, Thuc Tri Nguyen, Son Truong Nguyen, Ihtisham Bukhari
Oxidative Medicine and Cellular Longevity.2023; 2023: 1. CrossRef - A Systematic Review and Meta-Analysis Comparing the Diagnostic Accuracy Tests of COVID-19
Juan Jeferson Vilca-Alosilla, Mayron Antonio Candia-Puma, Katiusca Coronel-Monje, Luis Daniel Goyzueta-Mamani, Alexsandro Sobreira Galdino, Ricardo Andrez Machado-de-Ávila, Rodolfo Cordeiro Giunchetti, Eduardo Antonio Ferraz Coelho, Miguel Angel Chávez-Fu
Diagnostics.2023; 13(9): 1549. CrossRef - Prediction Models for Intrauterine Growth Restriction Using Artificial Intelligence and Machine Learning: A Systematic Review and Meta-Analysis
Riccardo Rescinito, Matteo Ratti, Anil Babu Payedimarri, Massimiliano Panella
Healthcare.2023; 11(11): 1617. CrossRef - Machine learning algorithms for diagnosis of hip bone osteoporosis: a systematic review and meta-analysis study
Fakher Rahim, Amin Zaki Zadeh, Pouya Javanmardi, Temitope Emmanuel Komolafe, Mohammad Khalafi, Ali Arjomandi, Haniye Alsadat Ghofrani, Kiarash Shirbandi
BioMedical Engineering OnLine.2023;[Epub] CrossRef - Diagnostic accuracy of biomarkers to detect acute mesenteric ischaemia in adult patients: a systematic review and meta-analysis
Annika Reintam Blaser, Joel Starkopf, Martin Björck, Alastair Forbes, Karri Kase, Ele Kiisk, Kaja-Triin Laisaar, Vladislav Mihnovits, Marko Murruste, Merli Mändul, Anna-Liisa Voomets, Kadri Tamme
World Journal of Emergency Surgery.2023;[Epub] CrossRef - The utility of long non-coding RNAs in chronic obstructive pulmonary disease: a comprehensive analysis
Qi Lin, Chaofeng Zhang, Huixin Weng, Yating Lin, Yucang Lin, Zhipeng Ruan
BMC Pulmonary Medicine.2023;[Epub] CrossRef - Diagnostic accuracy of whole-body magnetic resonance imaging versus positron emission tomography-computed tomography for the staging of pediatric lymphoma: a systematic review and meta-analysis
Deeksha Bhalla, Manisha Jana, Devasenathipathy Kandasamy
Pediatric Radiology.2023; 53(13): 2683. CrossRef - Diagnostic test accuracy of machine learning algorithms for the detection intracranial hemorrhage: a systematic review and meta-analysis study
Masoud Maghami, Shahab Aldin Sattari, Marziyeh Tahmasbi, Pegah Panahi, Javad Mozafari, Kiarash Shirbandi
BioMedical Engineering OnLine.2023;[Epub] CrossRef - Diagnostic performance of CL Detect rapid-immunochromatographic test for cutaneous leishmaniasis: a systematic review and meta-analysis
Behailu Taye Gebremeskele, Gashaw Adane, Mohammed Adem, Fitsumbrhan Tajebe
Systematic Reviews.2023;[Epub] CrossRef - Reliability of machine learning to diagnose pediatric obstructive sleep apnea: Systematic review and meta‐analysis
Gonzalo C. Gutiérrez‐Tobal, Daniel Álvarez, Leila Kheirandish‐Gozal, Félix del Campo, David Gozal, Roberto Hornero
Pediatric Pulmonology.2022; 57(8): 1931. CrossRef - How to Analyze the Diagnostic Performance of a New Test? Explained with Illustrations
Deepak Dhamnetiya, Ravi Prakash Jha, Shalini Shalini, Krittika Bhattacharyya
Journal of Laboratory Physicians.2022; 14(01): 090. CrossRef - Diagnostic accuracy of magnetic resonance imaging targeted biopsy techniques compared to transrectal ultrasound guided biopsy of the prostate: a systematic review and meta-analysis
E. J. Bass, A. Pantovic, M. J. Connor, S. Loeb, A. R. Rastinehad, M. Winkler, Rhian Gabe, H. U. Ahmed
Prostate Cancer and Prostatic Diseases.2022; 25(2): 174. CrossRef - Diagnostic performance and prognostic impact of coronary angiography‐based Index of Microcirculatory Resistance assessment: A systematic review and meta‐analysis
Weijia Li, Tatsunori Takahashi, Saul A. Rios, Azeem Latib, Joo Myung Lee, William F. Fearon, Yuhei Kobayashi
Catheterization and Cardiovascular Interventions.2022; 99(2): 286. CrossRef - Assessing the Knowledge of the Osteopathic Profession in New York City’s Eastern European Communities
Justin Chin, Lina Kleyn, Emily Dube, Mark Terrell, Christine M Lomiguen, Mikhail Volokitin
Cureus.2022;[Epub] CrossRef - The diagnostic accuracy of clinical tests for anterior cruciate ligament tears are comparable but the Lachman test has been previously overestimated: a systematic review and meta-analysis
Pawel A. Sokal, Richard Norris, Thomas W. Maddox, Rachel A. Oldershaw
Knee Surgery, Sports Traumatology, Arthroscopy.2022; 30(10): 3287. CrossRef - Comparison of Diagnostic Test Accuracy of Cone-Beam Breast Computed Tomography and Digital Breast Tomosynthesis for Breast Cancer: A Systematic Review and Meta-Analysis Approach
Temitope Emmanuel Komolafe, Cheng Zhang, Oluwatosin Atinuke Olagbaju, Gang Yuan, Qiang Du, Ming Li, Jian Zheng, Xiaodong Yang
Sensors.2022; 22(9): 3594. CrossRef - Clinical Validity of 16α-[18F]Fluoro-17β-Estradiol Positron Emission Tomography/Computed Tomography to Assess Estrogen Receptor Status in Newly Diagnosed Metastatic Breast Cancer
Jasper J.L. van Geel, Jorianne Boers, Sjoerd G. Elias, Andor W.J.M. Glaudemans, Erik F.J. de Vries, Geke A.P. Hospers, Michel van Kruchten, Evelien J.M. Kuip, Agnes Jager, Willemien C. Menke-van der Houven van Oordt, Bert van der Vegt, Elisabeth G.E. de V
Journal of Clinical Oncology.2022; 40(31): 3642. CrossRef - Diagnostic Performance of Antigen Rapid Diagnostic Tests, Chest Computed Tomography, and Lung Point-of-Care-Ultrasonography for SARS-CoV-2 Compared with RT-PCR Testing: A Systematic Review and Network Meta-Analysis
Sung Ryul Shim, Seong-Jang Kim, Myunghee Hong, Jonghoo Lee, Min-Gyu Kang, Hyun Wook Han
Diagnostics.2022; 12(6): 1302. CrossRef - Diagnostic Accuracy of Machine Learning Models on Mammography in Breast Cancer Classification: A Meta-Analysis
Tengku Muhammad Hanis, Md Asiful Islam, Kamarul Imran Musa
Diagnostics.2022; 12(7): 1643. CrossRef - Association of No Evidence of Disease Activity With No Long-term Disability Progression in Multiple Sclerosis
Dalia Rotstein, Jacqueline Madeleine Solomon, Maria Pia Sormani, Xavier Montalban, Xiang Y. Ye, Dina Dababneh, Alexandra Muccilli, Prakesh Shah
Neurology.2022;[Epub] CrossRef - Prospective study of Na[18F]F PET/CT for cancer staging in morbidly obese patients compared with [99mTc]Tc-MDP whole-body planar, SPECT and SPECT/CT
Sharjeel Usmani, Najeeb Ahmed, Gopinath Gnanasegaran, Fareeda Al kandari, Fahad Marafi, Ahmed Bani-Mustafa, Ahmed Musbah, Maryam Jassem Almashmoum, Tim Van den Wyngaert
Acta Oncologica.2022; 61(10): 1230. CrossRef - Structured data vs. unstructured data in machine learning prediction models for suicidal behaviors: A systematic review and meta-analysis
Danielle Hopkins, Debra J. Rickwood, David J. Hallford, Clare Watsford
Frontiers in Digital Health.2022;[Epub] CrossRef - Growth Differentiation Factor-15 as a Candidate Biomarker in Gynecologic Malignancies: A Meta-analysis
Dipayan Roy, Anupama Modi, Purvi Purohit, Manoj Khokhar, Manu Goyal, Shailja Sharma, Puneet Setia, Antonio Facciorusso, Praveen Sharma
Cancer Investigation.2022; 40(10): 901. CrossRef - Diagnostic accuracy of MRI techniques for treatment response evaluation in patients with brain metastasis: A systematic review and meta-analysis
Wouter H.T. Teunissen, Chris W. Govaerts, Miranda C.A. Kramer, Jeremy A. Labrecque, Marion Smits, Linda Dirven, Anouk van der Hoorn
Radiotherapy and Oncology.2022; 177: 121. CrossRef - Accuracy of Diagnostic Tests for the Detection of Chagas Disease: A Systematic Review and Meta-Analysis
Mayron Antonio Candia-Puma, Laura Yesenia Machaca-Luque, Brychs Milagros Roque-Pumahuanca, Alexsandro Sobreira Galdino, Rodolfo Cordeiro Giunchetti, Eduardo Antonio Ferraz Coelho, Miguel Angel Chávez-Fumagalli
Diagnostics.2022; 12(11): 2752. CrossRef - Assessment of the accuracy of 11 different diagnostic tests for the detection of Schistosomiasis mansoni in individuals from a Brazilian area of low endemicity using latent class analysis
Silvia Gonçalves Mesquita, Roberta Lima Caldeira, Tereza Cristina Favre, Cristiano Lara Massara, Lílian Christina Nóbrega Holsbach Beck, Taynãna César Simões, Gardênia Braz Figueiredo de Carvalho, Flória Gabriela dos Santos Neves, Gabriela de Oliveira, La
Frontiers in Microbiology.2022;[Epub] CrossRef - Diagnosis of pathological conditions through electronic nose analysis of urine samples: a systematic review and meta-analysis
Helga A.S. Afonso, Mariana V. Farraia, Mónica A. Vieira, João Cavaleiro Rufo
Porto Biomedical Journal.2022; 7(6): e188. CrossRef - Meta-analysis of diagnostic test accuracy studies with multiple thresholds for data integration
Sung Ryul Shim
Epidemiology and Health.2022; 44: e2022083. CrossRef - A systematic review and meta-analysis of the diagnostic accuracy of biparametric prostate MRI for prostate cancer in men at risk
E. J. Bass, A. Pantovic, M. Connor, R. Gabe, A. R. Padhani, A. Rockall, H. Sokhi, H. Tam, M. Winkler, H. U. Ahmed
Prostate Cancer and Prostatic Diseases.2021; 24(3): 596. CrossRef - Diagnosis of Alzheimer’s Disease in Developed and Developing Countries: Systematic Review and Meta-Analysis of Diagnostic Test Accuracy
Miguel A. Chávez-Fumagalli, Pallavi Shrivastava, Jorge A. Aguilar-Pineda, Rita Nieto-Montesinos, Gonzalo Davila Del-Carpio, Antero Peralta-Mestas, Claudia Caracela-Zeballos, Guillermo Valdez-Lazo, Victor Fernandez-Macedo, Alejandro Pino-Figueroa, Karin J.
Journal of Alzheimer's Disease Reports.2021; 5(1): 15. CrossRef - Breath biopsy of breast cancer using sensor array signals and machine learning analysis
Hsiao-Yu Yang, Yi-Chia Wang, Hsin-Yi Peng, Chi-Hsiang Huang
Scientific Reports.2021;[Epub] CrossRef - Meta-Analysis and Systematic Review of the Application of Machine Learning Classifiers in Biomedical Applications of Infrared Thermography
Carolina Magalhaes, Joaquim Mendes, Ricardo Vardasca
Applied Sciences.2021; 11(2): 842. CrossRef - Predicting Clinical Outcomes in Acute Ischemic Stroke Patients Undergoing Endovascular Thrombectomy with Machine Learning
Yao Hao Teo, Isis Claire Z. Y. Lim, Fan Shuen Tseng, Yao Neng Teo, Cheryl Shumin Kow, Zi Hui Celeste Ng, Nyein Chan Ko Ko, Ching-Hui Sia, Aloysius S. T. Leow, Wesley Yeung, Wan Yee Kong, Bernard P. L. Chan, Vijay K. Sharma, Leonard L. L. Yeo, Benjamin Y.
Clinical Neuroradiology.2021; 31(4): 1121. CrossRef - Application of artificial intelligence in diagnosis of osteoporosis using medical images: a systematic review and meta-analysis
L. Gao, T. Jiao, Q. Feng, W. Wang
Osteoporosis International.2021; 32(7): 1279. CrossRef - The Accuracy of Visceral Adiposity Index for the Screening of Metabolic Syndrome: A Systematic Review and Meta-Analysis
Moniba Bijari, Sara Jangjoo, Nima Emami, Sara Raji, Mahdi Mottaghi, Roya Moallem, Ali Jangjoo, Amin Saberi, Pawel Grzmil
International Journal of Endocrinology.2021; 2021: 1. CrossRef - Immunofluorescence Targeting PBP2a Protein: A New Potential Methicillin Resistance Screening Test
Serenella Silvestri, Elisa Rampacci, Valentina Stefanetti, Michele Trotta, Caterina Fani, Lucia Levorato, Chiara Brachelente, Fabrizio Passamonti
Frontiers in Veterinary Science.2021;[Epub] CrossRef - Accuracy of malaria diagnostic tests performed on non-invasively collected samples: a systematic review and meta-analysis
Celestin Danwang, Jean Jacques Noubiap, Jacob Souopgui, Jean Gaudart, Jean Cyr Yombi, Annie Robert
BMJ Global Health.2021; 6(6): e005634. CrossRef - Perceptions of the osteopathic profession in New York City’s Chinese Communities
Justin Chin, Sarah Li, Gregory Yim, YaQun Arlene Zhou, Peter Justin Wan, Emily R Dube, Mikhail Volokitin, Sonu Sahni, Mark A Terrell, Christine M Lomiguen
Family Medicine and Community Health.2020; 8(1): e000248. CrossRef - Perceptions of the Osteopathic Profession in New York City's Korean Communities
Justin Chin, DO, Haeinn Woo, OMS-IV, Diane Choi, OMS-III, Emily Dube, MS, Mikhail Volokitin, MD, DO, Christine Lomiguen, MD
Osteopathic Family Physician.2020; 13(1): 12. CrossRef - Development of a voiding diary using urination recognition technology in mobile environment
Gun Hyun Park, Su Jin Kim, Young Sam Cho
Journal of Exercise Rehabilitation.2020; 16(6): 529. CrossRef
PubReader
ePub Link
Cite
XML DownloadDiagnostic test accuracy: application and practice using R software
Figure 1. Summary statistics for diagnostic test accuracy.
Figure 2. Flow chart of diagnostic test accuracy (DTA) using R “mada” & “meta” package. TP, true positive; FP, false positive; FN, false negative; TN, true negative; DOR, diagnostic odds ratio; SROC, summary receiver operating characteristic.
Figure 3. Univariate analysis: sensitivity. CI, confidence interval; g, subgroup.
Figure 4. Univariate analysis: diagnostic odds ratio. OR, odds ratio; CI, confidence interval; g, subgroup.
Figure 5. Summary receiver operating characteristic (SROC) curve (bivariate model) for diagnostic test accuracy. CI, confidence interval; AUC, area under the curve; DOR, diagnostic odds ratio.
Figure 1.
Figure 2.
Figure 3.
Figure 4.
Figure 5.
Diagnostic test accuracy: application and practice using R software
| Summary statistics | Equation | Definition |
|---|---|---|
| Sn | TP/(TP+FN) | Proportion of persons who have positive test results to those with disease |
| Sp | TN/(FP+TN) | Proportion of persons who have negative test result to those without disease |
| PPV | TP/(TP+FP) | Proportion of persons with disease to those who have positive test result |
| NPV | TN/(FN+TN) | Proportion of persons without disease to those who have negative test result |
| LR+ | Sn/(1-Sp) | Ratio of the probability of a positive test result among those with disease to that of a positive test result among those without disease |
| LR- | (1-Sn)/Sp | Ratio of the probability of a negative test result among those with disease to that of a negative test result among those without disease |
| Accuracy of index test | (TP+TN)/(TP+FP+FN+TN) | The proportion of persons who are true positive and persons who are true negative among all subjects |
| DOR | (TP*TN)/(FP*FN) | The ratio of the OR for a positive test result among persons with disease to that among persons without disease |
| Id | TP | FP | FN | TN | g |
|---|---|---|---|---|---|
| Wiegmann | 21 | 1 | 9 | 104 | 1 |
| Bouhanick | 49 | 21 | 7 | 110 | 1 |
| Schwab | 24 | 5 | 3 | 31 | 1 |
| Zelmanovitz | 39 | 6 | 5 | 48 | 0 |
| Ahn | 23 | 9 | 7 | 41 | 0 |
| Ng | 12 | 7 | 2 | 44 | 0 |
| Gansevoort | 10 | 13 | 3 | 40 | 1 |
| Incerti | 82 | 12 | 7 | 177 | 0 |
| Sampaio | 99 | 45 | 21 | 128 | 0 |
Table 1. Diagnostic test accuracy summary statistics [2]
Sn, sensitivity; Sp, specificity; PPV, positive predictive value; NPV, negative predictive value; LR+, positive likelihood ratio; LR-, negative likelihood ratio; DOR, diagnostic odds ratio; TP, true positive; FP, false positive; FN, false negative; TN, true negative; OR, odds ratio.
Table 2. Sample data for diagnostic test accuracy [2]
TP, true positive; FP, false positive; FN, false negative; TN, true negative; g, subgroup.
